A mathematical problem requires students to reach a solutiw:on that does not
involve simply the application of a standard procedure or algorithm. An example
is shown belo
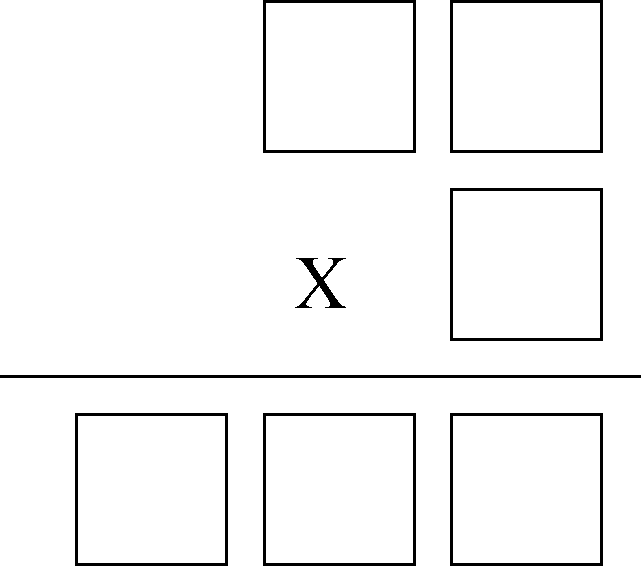
Using each digit only once, can you place 1, 2, 3, 4, 5, 6 into the squares
below so that the multiplication problem is correct?

In solving such problems students are likely to use strategies or heuristics
such as drawing a table, estimating, looking and finding a pattern, listing
possibilities, and so on. The choosing and using of these strategies provides
an indication of how good the students are at solving mathematical problems.
Performance criteria to assess problem solving can be developed to indicate
the depth of mathematical knowledge on a particular task. This may take the
form of a rubric. For example, a rubric for problem solving might be a C grade
for a response that was complete but shows no extension. B grade would be indicated
by a solution that is well presented and indicated good understanding. An A
grade would be for students who formed generalisations and indicated extensions
of the problem. Many different rubrics have been suggested, however, these can
also be developed and agreed to by the teacher working in conjunction with students.

The school I was at always gave students an investigation followed by a test one week later. The purpose of this test was to ensure that the students understood the problem and how to obtain an answer. It also made sure the students understood the problem and had not just copied the answer.
When first given the investigation students are advised on what is expected, for example, algebraic results or essay answers; when the test would be; and who they can seek for assistance. In most cases students could work in groups; could only ask the teacher a question on the investigation outside class time; and only up until the day before the investigation was due.
On the day of the test the investigation that they had done at home was collected and another copy of the question was handed to the students. They were then given 40-80 minutes, depending on the investigation, to finish it.
The advantage of using this method is that the teacher can easily see who has attempted the problem and who understands it. The disadvantages are that some students aren’t good in test situations and the result may not reflect the work they put in. Students were given as much time as they needed (up to 80 minutes) to complete the test.
(Maggie, student teacher)
An interview with Alan Schoenfeld
 How do you
assess that Mathematical problem solving?
How do you
assess that Mathematical problem solving?
A few quick thoughts here (for real detail, see my book Mathematical Problem
Solving). These comments serve as a gloss on the substance contained in the
book. First, my basic premise: if you want to assess students' problem-solving
abilities, you have to give them the opportunity to do some real problem solving.
Thus in my problem solving course, the mid-term exam and the final are each
two-week long, take-home exams, containing ten problems.
Second main point: your grading scheme has to reflect the values you want to
promote. Thus, for example, I ask students to tell me about approaches they
tried, even if they weren't successful; I give multiple credit for multiple
solutions; and I give a lot of extra credit for extensions and generalizations
of my problems that the students create.
 |
 |
 |